Πεπερασμένα Αυτόματα (DFA)

Τα Πεπερασμένα Αυτόματα (Deterministic Finite Automata – DFA) αποτελούν θεμελιώδη έννοια της Θεωρίας Υπολογισμού και χρησιμοποιούνται για την αναγνώριση γλωσσών. Με απλά λόγια, ένα DFA είναι ένα μαθηματικό μοντέλο που περιγράφει έναν “μηχανισμό” ο οποίος δέχεται ή απορρίπτει συμβολοσειρές (strings), ανάλογα με το αν αυτές ανήκουν στη γλώσσα που αναγνωρίζει.

Ένα DFA ορίζεται από 5 στοιχεία (πεντάδα):

1. Q: Πεπερασμένο σύνολο καταστάσεων
2. Σ: Αλφάβητο (σύνολο συμβόλων εισόδου)
3. δ: Συνάρτηση μετάβασης (Q × Σ → Q)
4. q₀: Αρχική κατάσταση (q₀ ∈ Q)
5. F: Σύνολο τελικών/αποδεκτών καταστάσεων (F ⊆ Q)

Η λειτουργία είναι ντετερμινιστική, δηλαδή για κάθε κατάσταση και κάθε σύμβολο εισόδου υπάρχει μία μόνο πιθανή μετάβαση. Τα Deterministic Finite Automata (DFA) μοντελοποιούν υπολογιστικά συστήματα με πεπερασμένη μνήμη. Μπορούν να αναγνωρίσουν μόνο κανονικές γλώσσες (π.χ. αν μια λέξη τελειώνει σε “01”). Δεν μπορούν όμως να λύσουν προβλήματα που απαιτούν “μέτρημα” χωρίς όριο (π.χ. αν ο αριθμός των 0 ισούται με τον αριθμό των 1).

Πώς λειτουργεί το DFA;

Το DFA ξεκινά από την αρχική κατάσταση και «διαβάζει» τα σύμβολα της εισόδου ένα-ένα.

• Κάθε σύμβολο οδηγεί σε μία μετάβαση σε νέα κατάσταση (σύμφωνα με τον πίνακα μετάβασης).
• Όταν τελειώσει η είσοδος, ελέγχουμε αν βρισκόμαστε σε κατάσταση που ανήκει στο σύνολο F.
• Αν ναι → η συμβολοσειρά γίνεται αποδεκτή.
• Αν όχι → απορρίπτεται.

Παράδειγμα DFA

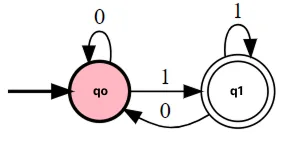
Πρόβλημα: Σχεδιάζουμε DFA που δέχεται όλες τις συμβολοσειρές πάνω στο αλφάβητο {0,1}, οι οποίες τελειώνουν με το σύμβολο 1. Φαντάσου ότι φτιάχνουμε μια εφαρμογή (π.χ. web form) και θέλουμε να ελέγχουμε αν ο χρήστης πληκτρολογεί έναν δυαδικό αριθμό που τελειώνει σε 1. Στο ακόλουθο παράδειγμα δεν ασχολούμαστε πως εισάγωνται τα δεδομένα, ούτε επίσης πως αποθηκεύονται.

Ορισμός DFA:

• Q = {q₀, q₁}
• Σ = {0,1}
• q₀ = αρχική κατάσταση
• F = {q₁} τελική κατάστασ

Μεταβάσεις (δ):

• Από q₀:
  • με 0 → μένει στο q₀
  • με 1 → πάει στο q₁
• Από q₁:
  • με 0 → πάει στο q₀
  • με 1 → μένει στο q₁

Διάγραμμα Καταστάσεων:

Python – εφαρμογή

import re
# Καταστάσεις: q0 = 0, q1 = 1
pattern = re.compile(r'(0|1)*1$')

# Τεστ εισόδων
print(bool(pattern.fullmatch("101")))  # True
print(bool(pattern.fullmatch("100")))  # False
print(bool(pattern.fullmatch("1111"))) # True
print(bool(pattern.fullmatch("000")))  # False

def dfa_ends_with_one(input_string):
    # Καταστάσεις: q0 = 0, q1 = 1
    state = 0  # q0 (αρχική κατάσταση)

    for char in input_string:
        if char == '0':
            state = 0  # μετάβαση στο q0
        elif char == '1':
            state = 1  # μετάβαση στο q1
        else:
            return False  # αν μη αποδεκτός χαρακτήρας
# Επιστρέφει True αν βρ. σε τελική κατάσταση (q1)
    return state == 1

# Παραδείγματα
print(dfa_ends_with_one("101"))  # True (δέχεται)
print(dfa_ends_with_one("100"))  # False (απορρίπτει)

SQL – εφαρμογή

Εστω πίνακας “sample” με στήλες: id και binary_string και που έχουμε αποθηκευσει τα δεδομένα: “101”,”100″,”1111″,”000″ ή και όποια άλλα θέλετε

SELECT id, binary_string
FROM sample
WHERE binary_string REGEXP '^(0|1)*1$';

SELECT binary_string
FROM sample
WHERE binary_string LIKE '%1';

Λειτουργικά Συστήματα – εφαρμογή

Εστω αρχείο “numbers.txt” με τα δεδομένα: “101”,”100″,”1111″,”000″ ή και όποια άλλα θέλετε

Get-Content numbers.txt | Where-Object { $_ -match '^(0|1)*1$' }

grep -E '^(0|1)*1$' numbers.txt

Τα DFA είναι ισχυρά μαθηματικά εργαλεία για την αναγνώριση κανονικών γλωσσών. Χρησιμοποιούνται σε συμπιεστές, γλωσσικούς αναλυτές, firewalls, αλλά και ως “χαρτογράφηση” του τι γίνεται απλό ή αδύνατο με περιορισμένους πόρους. Γενικότερα, χρησιμοποιούνται σε τομείς όπως:

• Αναγνώριση μοτίβων (pattern matching)
• Σχεδιασμός μεταγλωττιστών (compilers)
• Επεξεργασία κειμένου και δεδομένων

Με την απλότητα και τη μαθηματική τους ακρίβεια, τα DFA αποτελούν το πρώτο βήμα για να κατανοήσουμε πιο σύνθετα υπολογιστικά μοντέλα.

Σχετιζόμενο Ακαδημαικό Πρόγραμμα