Δυναμικός Προγραμματισμός - INFORMIX "Ο Πληροφορικός"

Mέρος 2ο: Κατανόηση χρησιμότητας Δυναμικού προγραμματισμού

Ο Δυναμικός Προγραμματισμός (Dynamic Programming) είναι μια υπολογιστική μέθοδος που χρησιμοποιείται για την επίλυση προβλημάτων που μπορούν να αναλυθούν σε υποπροβλήματα. Αντί να επαναλαμβάνει υπολογισμούς για κοινά υποπροβλήματα, ο δυναμικός προγραμματισμός αποθηκεύει τα αποτελέσματα των υπολογισμών αυτών και τα επαναχρησιμοποιεί όταν χρειάζεται, βελτιστοποιώντας έτσι την απόδοση του αλγορίθμου.

Όταν έχουμε ένα πρόβλημα που έχει τις εξής ιδιότητες:

Ιδιότητα των Βέλτιστων Επιμέρους Δομών: για να λύσουμε το πρόβλημα αρκεί να υπολογίσουμε την βέλτιστη λύση σε κάποια υποπροβλήματα. συνήθως με αναδρομή.
Μικρός Αριθμός Υποπροβλημάτων: Το πλήθος των υποπροβλημάτων που πρέπει να λύσουμε είναι μικρό (δηλαδή πολυωνυμικό ως προς το μέγεθος του προβλήματος)
Επικαλυπτόμενα Επιμέρους Προβλήματα: Ότι λύνουμε πολλές φορές τα ίδια
υποπροβλήματα με αποτέλεσμα να χάνουμε χρόνο

Ο Δυναμικός Προγραμματισμός (Dynamic Programming – DP) είναι όχι απλώς επίκαιρος, αλλά παραμένει μία από τις θεμελιώδεις και ισχυρότερες αλγοριθμικές τεχνικές στην επιστήμη των υπολογιστών και σε πολλούς άλλους τομείς

Δύο Βασικές Προσεγγίσεις

Ο δυναμικός προγραμματισμός υλοποιείται συνήθως με δύο τρόπους:

Memoization (Top-Down): Είναι μια αναδρομική προσέγγιση που αποθηκεύει τα αποτελέσματα των υπολογισμένων υπο-προβλημάτων σε έναν πίνακα (ή λεξικό), ώστε να μην τα επανυπολογίσει. Είναι πιο κοντά στην αρχική αναδρομική σκέψη.
Bottom-Up (Tabulation): Είναι μια επαναληπτική προσέγγιση που λύνει τα υπο-προβλήματα από τις μικρότερες τιμές προς τις μεγαλύτερες, γεμίζοντας έναν πίνακα με τις λύσεις. Είναι συχνά πιο αποδοτική σε χώρο και χρόνο, καθώς αποφεύγει το overhead της αναδρομής.

Και οι δύο προσεγγίσεις οδηγούν στην ίδια βελτιστοποιημένη πολυπλοκότητα. Στην προκείμενη περίπτωση για τον αλγόριθμο του Fibonacci θα τον μελετήσουμε με τον Memoization (Top-Down) τρόπο. Προκύπτει ο ακόλουθος ψευδοκώδικας:

ΣΥΝΑΡΤΗΣΗ Fibonacci(n)
  ΕΑΝ ΥΠΑΡΧΕΙ ΣΤΗ ΜΝΗΜΗ[n] ΤΟΤΕ
    ΕΠΕΣΤΡΕΨΕ ΜΝΗΜΗ[n]
  ΤΕΛΟΣ
  ΕΙΔΑΛΛΩΣ
    ΕΑΝ n == 0 ή n == 1 ΤΟΤΕ
      αποτέλεσμα ← 1
    ΕΙΔΑΛΛΩΣ
      αποτέλεσμα ← Fibonacci(n-1) + Fibonacci(n-2) //άθροισμα προηγ. αριθμών 
    ΤΕΛΟΣ
    ΜΝΗΜΗ[n] ← αποτέλεσμα
    ΕΠΕΣΤΡΕΨΕ αποτέλεσμα
ΤΕΛΟΣ

Με την αποθήκευση των ενδιάμεσων λύσεων – αποτελεσμάτων η συνάρτηση fib(k) υπολογίζεται μία φορά και αποθηκεύεται για μελλοντική χρήση. Άρα δεν έχουμε δυαδικό δέντρο κλήσεων, αλλά γραμμική αλυσίδα με αναδρομική εξίσωση T(n) = T(n-1)+C (όπου C είναι μια σταθερά για τις βασικές λειτουργίες εκτός των αναδρομικών κλήσεων).

Η παραπάνω αναδρομική σχέση μπορεί να υπολογισθεί με την μέθοδο της επανάληψης

Tnew(n) = Tnew(n-1) + C Tnew(n-1) = Tnew(n-2) + 2C Tnew(n-2) = Tnew(n-3) + 3C
…

Παρατηρούμε ένα μοτίβο. Κάθε φορά που ανοίγει η αναδρομή, ο συντελεστής του C αυξάνεται κατά 1, και ο δείκτης του T μειώνεται κατά 1. Συμπεραίνω ότι μετά από k επαναλήψεις, η σχέση θα είναι:
Τnew(n-k) = Tnew(n-k) + kC

Φτανουμε στην βασική περίπτωση που ειναι η Tnew(0). Αυτό συμβαίνει όταν n−k=0, δηλαδή όταν k=n. Αντικαθιστώντας k=n στην αναδρομική εξίσωση:
Τnew(n) = Tnew(n-n) + nC = T(0) + nC. Γνωρίζω ότι T(0)=1 δηλαδή μια άλλη σταθερά, επομένως Τnew(n) = Cother + nC

Επειδή το Cother και το C είναι σταθερές, ο κυρίαρχος όρος είναι το nC. Στον συμβολισμό Big O notation ή Θ, αυτό σημαίνει ότι η χρονική πολυπλοκότητα είναι: Tnew(n) = Θ(n)

Σύμφωνα με την θεωρία n < 2ⁿ συμπεραίνω ότι ο νέος αλγόριθμος είναι καλύτερος απο τον αρχικό

Εκδοχή βελτιστοποίησης αλγορίθμου με memoization (`@lru_cache`)

# αποθηκεύει αυτόματα το αποτέλεσμα μιας συνάρτησης κάθε φορά που αυτή καλείται 
# με συγκεκριμένα ορίσματα (arguments). Αν ξανακληθεί με τα ίδια ορίσματα, 
# δεν εκτελεί ξανά τον υπολογισμό, αλλά επιστρέφει το αποθηκευμένο (cached) αποτέλεσμα.

from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
    if n == 0 or n == 1:
        return 1
    return fib(n - 1) + fib(n - 2)

Η συνάρτηση καλεί: fib(n-1) και fib(n-2) αλλά χάρη στη cache (μνήμη), κάθε fib(k) καλείται μόνο μία φορά για κάθε k στο διάστημα [0, n]

Εκτέλεση του αλγορίθμου και εμφάνιση απαιτούμενου χρόνου εκτέλεσης

Για τον δειγματισμό επιλέχθηκαν (1) στο σύννεφο μέσω του Google Colab kai (2) τοπικά με το Ms VsCode

Για τον αριθμό σαράντα (40) παρατηρούμε:

Colab (cloud): T(n) < 1m απεικονιζεται ως 0s | από 26s απεικονιζεται ως 0s
VsCode (local): T(n) = 1.21s | από 27.33s

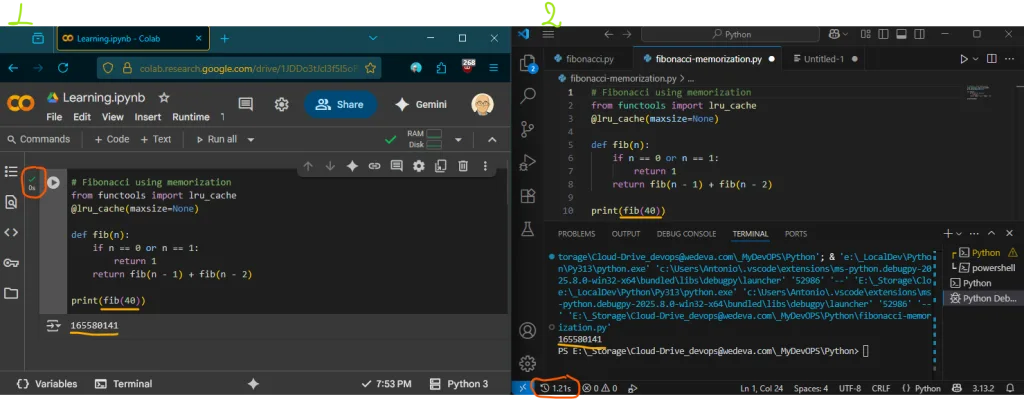
Συμπέρασμα

Με την τεχνική του Δυναμικού Προγραμματισμού πετύχαμε αισθητή μείωση του χρόνου εκτέλεσης του αλγορίθμου (στο παράδειγμα απο 27.33s σε 1.21s). Η memoization είναι πολλαπλάσια ταχύτερη από την απλή αναδρομή, ειδικά για μεγαλύτερες τιμές. Για να γίνει εμφανέστερη η διαφορά αποτελέσματος εκτέλεσης αλγορίθμου με χρονική πολυπλοκότητα εκθετική (n^kati) σε πολυωνυμικη (n) παραθέτω ακόλουθα στιγμιότυπο για τον αριθμό πενήντα (50).

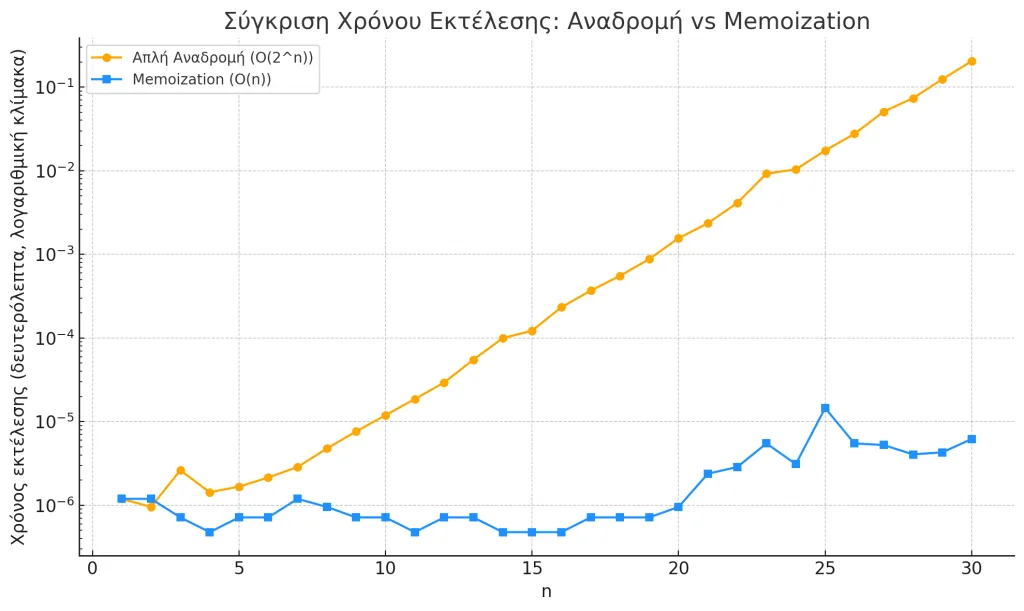
Πορτοκαλί καμπύλη – Απλή Αναδρομή (O(2ⁿ)) – εκθετική:

Ο χρόνος εκτέλεσης αυξάνεται εκθετικά με το n.
Οι επαναλαμβανόμενες κλήσεις κάνουν τον αλγόριθμο αναποτελεσματικό μετά από ~n=30.

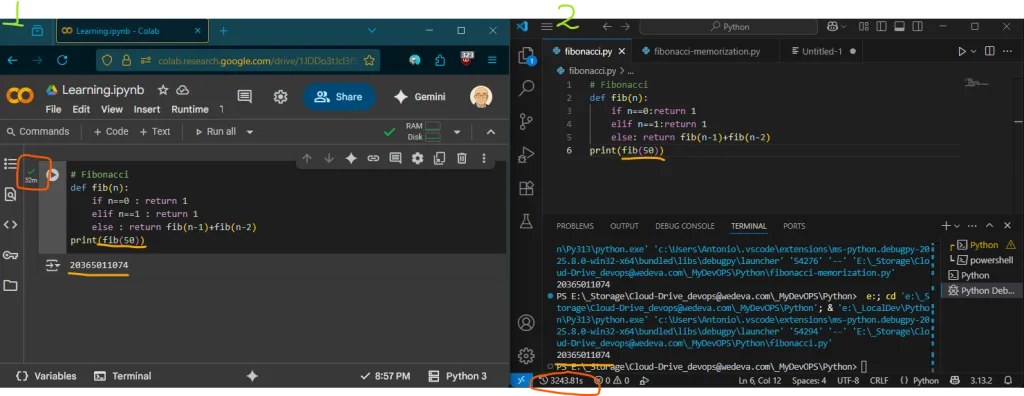
Για τον αριθμό πενήντα (50) παρατηρούμε:

Colab (cloud): T(n) = 52m
VsCode (local): T(n) = 3243.81s = 54.06m

Μπλε καμπύλη – Memoization (O(n)) – πολυωνυμική:

Ο χρόνος παραμένει σχεδόν σταθερός ή αυξάνεται γραμμικά.
Κάθε τιμή υπολογίζεται μία φορά, χάρη στην @lru_cache.

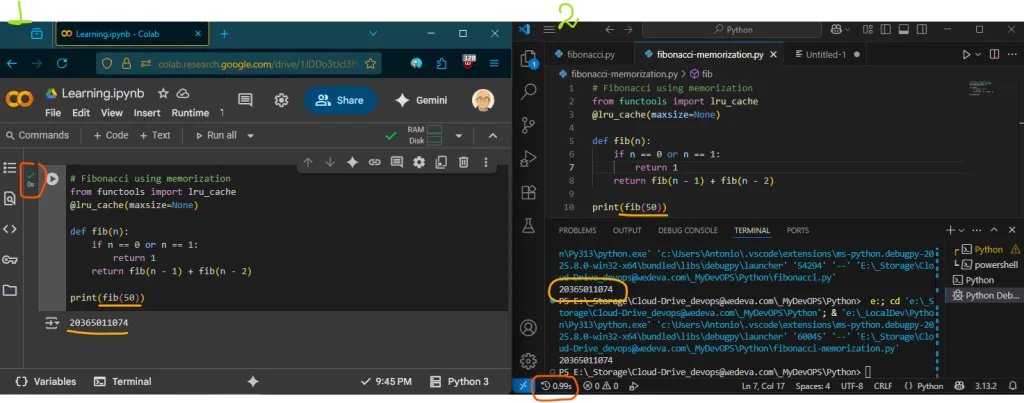
Για τον αριθμό πενήντα (50) παρατηρούμε:

Colab (cloud): T(n) < 1 min απεικονιζεται ως 0s
VsCode (local): T(n) = 1.19s

Για τον δειγματισμό επιλέχθηκαν (1) στο σύννεφο μέσω του Google Colab kai (2) τοπικά με το Ms VsCode

Σημείωση: ο χρόνος εκτέλεσης διαφέρει απο Colab (cloud) σε VsCode (local) διότι διαφορετική η διαθεσιμότητα πόρων (CPU, RAM) των δύο εργαλείων. Παρατηρήστε στην πορτοκαλί επισήμανση. ΠΡΟΣΟΧΗ η χρονική πολυπλοκότητα ΔΕΝ αλλάζει!

Συνοψίζοντας, ο Δυναμικός Προγραμματισμός δεν είναι απλώς επίκαιρος, αλλά ένα απαραίτητο εργαλείο για την επίλυση ενός ευρέος φάσματος πολύπλοκων προβλημάτων στον σύγχρονο κόσμο της τεχνολογίας. Η ικανότητα να αναγνωρίζεις πότε ένα πρόβλημα μπορεί να λυθεί με DP και να εφαρμόζεις σωστά τις τεχνικές του, είναι μια πολύτιμη δεξιότητα.

Παραπομπές:

Σχετιζόμενο Ακαδημαικό Πρόγραμμα

ΕΑΠ ΠΛΗ 30 Θεμελιώσεις Επιστήμης Υπολογιστών