Σήμερα όλοι μιλάμε για υπολογιστές, τεχνητή νοημοσύνη και εφαρμογές. Όμως, λίγοι γνωρίζουν ότι η βάση της Πληροφορικής δεν ξεκίνησε από ένα μηχάνημα, αλλά από μια ιδέα. Αυτή η ιδέα ανήκει στον Alan Turing και ονομάζεται Μηχανή Turing. ‘Ηταν το 1936, όταν ο Άγγλος μαθηματικός Alan Turing (1912-1954) εισήγαγε το ομώνυμο μοντέλο σε μια προσπάθεια τυποποίησης της έννοιας της αποτελεσματικής διερyασίας ή ισοδύναμα του αλγορίθμου ή και της τυποποίησης του υπολογιστή γενικού σκοπού.
Η Μηχανή Turing: Το «νοητικό εργαλείο» που γέννησε την Πληροφορική
Η Θεωρητική Πληροφορική μελετά τη φύση και τα όρια του υπολογισμού. Η Μηχανή Turing υπήρξε το πρώτο ολοκληρωμένο μαθηματικό μοντέλο που περιέγραψε με ακρίβεια τι σημαίνει «υπολογισμός» και ποιες διαδικασίες μπορούν να αυτοματοποιηθούν.
Τι είναι η Μηχανή Turing;
Η Μηχανή Turing δεν είναι υπολογιστής που μπορείς να δεις ή να αγγίξεις. Είναι ένα νοητικό μοντέλο που φαντάστηκε ο Τιούρινγκ το 1936 για να απαντήσει σε μια απλή αλλά τεράστια ερώτηση: Υπάρχει όριο στο τι μπορεί να υπολογίσει ένας άνθρωπος ή μια μηχανή;
Ένα τυπικό μοντέλο για την αποτελεσματική διεργασία πρέπει να έχει ορισμένες βασικές ιδιότητες.
- Πρώτα, μια διεργασία πρέπει να έχει πεπερασμένη περιγραφή, δηλαδή να ορίζεται με ένα πεπερασμένο πλήθος βημάτων υπολογισμού
- Δεύτερο, τα βήματα πρέπει να είναι διακριτά μεταξύ τους και το καθένα να μπορεί να εκτελείται μηχανιστικά σε πεπερασμένα χρόνο, ώστε να έχουμε τελικά ένα αποτέλεσμα, απ’ όπου και ο όρος αποτελεσματική διεργασία.
Δομικά στοιχεία μιας Μηχανής Turing
- Μονάδα Ελέγχου, ένας μηχανισμός πεπερασμένων καταστάσεων-μεταβάσεων που καθορίζουν τη συμπεριφορά της μηχανής και που έχει μια μοναδική τελική κατάσταση.
- Ταινία συμβόλων χωρισμένη σε κελιά-θέσεις, όπου καταγράφονται τα σύμβολα. Κάθε κελί-θέση μπορεί να περιέχει ένα σύμβολο από κάποιο αλφάβητο. Ως αρχή ορίζεται το αριστερότερο κελί και είναι απεριορίστου μήκους προς τα δεξιά (άπειρη). Συνήθως με # συμβολίζουμε το κενό κελί. Μ’ άλλα λόγια, η ταινία χρησιμεύει ως περιφερειακή μονάδα για είσοδο και έξοδο δεδομένων.
- Κεφαλή ανάγνωσης/εγγραφής, που δείχνει σε ένα συγκεκριμένο κελί-θέση και που μπορεί να κινείται αριστερά ή δεξιά.
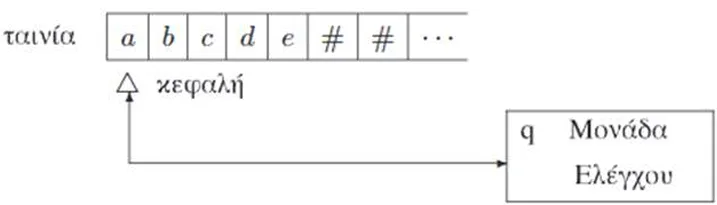
Με αυτά τα στοιχεία, η Μηχανή Turing μπορεί να προσομοιώσει κάθε αλγοριθμική διαδικασία. Μια μηχανή Turing μπορεί να έχει μία απο τις ακόλουθες συμπεριφορές.
- Να τερματίζει: όταν φτάνει στην μοναδική τελική κατάσταση (συμβολίζεται με h)
- Να πέφτει σε βρόχο – λούπα
- Να κρεμάει: αν π.χ. η κεφαλή είναι στο πρώτο κελί της ταινίας και γίνει μετάβαση αριστερά
Σημαντικό: Αποτελεί προγραμματιστικό λάθος να κρεμάει ή να πέφτει σε βρόγχο
Παράδειγμα: Αντιγραφή Συμβόλου.
Στο Αλφάβητο {A,Β} αν βρούμε ένα A στην ταινία, να το αντιγράψουμε στο πρώτο επόμενο κενό κελί.Η αρχική θέση της κεφαλής είναι στο αριστερότερο κελί. Η μηχανή Turing διατρέχει απο αριστερά προς τα δεξιά την ταινία. Αν συναντήσει το σύμβολο A το θυμάται και μεταβαίνει σε νέα κατάσταση και συνεχίζει δεξιά. Εάν συναντήσει κενό κελί # μεταβαίνει σε νέα κατάσταση και γράφει το A και αποδέχεται – σταματά.
Θεμελιώδη Συμβολή
Η εργασία του Turing (1936) απέδειξε ότι:
- Υπάρχουν προβλήματα που δεν είναι υπολογίσιμα, όπως το «πρόβλημα του τερματισμού» (halting problem).
- Η Μηχανή Turing είναι καθολικό μοντέλο: οποιοσδήποτε υπολογιστής μπορεί θεωρητικά να περιγραφεί με αυτό.
Η θεωρητική αυτή σύλληψη επηρέασε άμεσα τη δημιουργία των πρώτων ηλεκτρονικών υπολογιστών. Κατά τον Β΄ Παγκόσμιο Πόλεμο, ο Turing αξιοποίησε τις ιδέες του στην ανάπτυξη μηχανών αποκρυπτογράφησης (π.χ. Bombe) που συνέβαλαν στην αποκωδικοποίηση του γερμανικού συστήματος Enigma.
Σήμερα, η έννοια της Μηχανής Turing παραμένει κεντρική:
- Στη μελέτη της πολυπλοκότητας αλγορίθμων.
- Στην ανάπτυξη κβαντικών υπολογιστών, που επαναπροσδιορίζουν τα όρια της υπολογισιμότητας.
- Στη συζήτηση για την Τεχνητή Νοημοσύνη, με το γνωστό Τεστ Turing.
Το Βραβείο Turing
Ως αναγνώριση της τεράστιας συμβολής του Alan Turing, η Ένωση Υπολογιστικών Μηχανών (ACM) θέσπισε το Βραβείο Turing το 1966. Συχνά αποκαλείται και «Νόμπελ της Πληροφορικής», καθώς αποτελεί τη σημαντικότερη διεθνή διάκριση στον χώρο.
- Απονέμεται ετησίως σε ερευνητές που έχουν πραγματοποιήσει θεμελιώδη και διαχρονικά σημαντικά επιτεύγματα στην Πληροφορική.
- Συνοδεύεται από χρηματικό έπαθλο ύψους 1 εκατομμυρίου δολαρίων, με χορηγία της Google.
- Ανάμεσα στους βραβευμένους συγκαταλέγονται προσωπικότητες που έθεσαν τα θεμέλια του Ίντερνετ, της Τεχνητής Νοημοσύνης, των βάσεων δεδομένων και των γλωσσών προγραμματισμού.
Από τη Μηχανή Turing στο… επιτραπέζιο “Turing Machine”
Η ιδέα της Μηχανής Turing δεν ζει μόνο στα αμφιθέατρα, έχει εμπνεύσει και ένα σύγχρονο επιτραπέζιο παιχνίδι λογικής/επαγωγής, το Turing Machine. Οι παίκτες «ανακρίνουν» μια αναλογική πρωτο‑μηχανή μέσω διάτρητων καρτών (perforated cards) για να εντοπίσουν έναν μυστικό κωδικό με τον λιγότερο δυνατό αριθμό ερωτήσεων—μια πολύ προσιτή, παιγνιώδης εισαγωγή στις έννοιες της πληροφορίας, του ελέγχου υποθέσεων και της συστηματικής αναζήτησης.
Το επιτραπέζιο παιχνίδι “Turing Machine” βοηθά αναγνώστες χωρίς προϋπάρχουσες τεχνικές γνώσεις να νιώσουν πώς λειτουργεί ένας «κανόνας/μηχανή» που αξιολογεί ερωτήματα—ακριβώς όπως η Μηχανή Turing αφαιρετικά ορίζει τι σημαίνει υπολογισμός. Με άλλα λόγια, το παιχνίδι λειτουργεί ως διδακτικό γέφυρο από τη θεωρία στην πράξη. Αφορά Ηλικίες 14+ και έχει διακριθεί με Βραβεία & υποψηφιότητες καινοτομίας (Golden Geek 2023, As d’Or 2023 κ.ά.).
Η Μηχανή Turing απέδειξε ότι η έννοια του υπολογισμού μπορεί να περιγραφεί με απλούς κανόνες. Παρά τη θεωρητική της φύση, αποτελεί το θεμέλιο όλων των σύγχρονων υπολογιστικών συστημάτων και διατηρεί ακέραιη τη σημασία της στην έρευνα του 21ου αιώνα.



