Η πολυπλοκότητα αλγορίθμων, ή αλλιώς η χρονική πολυπλοκότητα (time complexity), μετρά το πόσο αυξάνεται ο χρόνος εκτέλεσης ενός αλγορίθμου καθώς αυξάνεται το μέγεθος της εισόδου. Συνήθως εκφράζεται χρησιμοποιώντας τον συμβολισμό (Big O notation) ή και ως Θ, ο οποίος περιγράφει την ασυμπτωτική ανώτερη οριακή τιμή της συνάρτησης του χρόνου εκτέλεσης.
Mέρος 1ο: Κατανόηση της Πολυπλοκότητας Αλγορίθμων με παράδειγμα για αλγόριθμο Fibonacci
Εχοντας αρχικά κατανοήσει τι είναι αλγόριθμος, ας αναλύσουμε την πολυπλοκότητα του αλγορίθμου Fibonacci, με βάση τον ορισμό:
# Fibonacci algorithm in Python
def fib(n):
if n == 0:
return 1
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)Υπολογισμός της Χρονικής Πολυπλοκότητας (Big O) ή Θ
Σχέση αναδρομής: Ο αριθμός των κλήσεων της συνάρτησης T(n) για τον υπολογισμό του fib(n) μπορεί να περιγραφεί από την εξής σχέση αναδρομής: T(n) = T(n-1)+T(n-2)+C (όπου C είναι μια σταθερά για τις βασικές λειτουργίες εκτός των αναδρομικών κλήσεων). Η παραπάνω αναδρομική σχέση μπορεί να υπολογισθεί μέσω φραγμάτων
Υπολογισμός ΑΝΩ Φράγματος
Γνωρίζω ότι το Θ(c) = 1 άρα προκύπτει η σχέση αναδρομής T(n) = T(n-1)+T(n-2)+1.
- Βρίσκω το ΑΝΩ φράγμα της αναδρομικής: Εντοπίζω τον μεγαλύτερο όρο από τους δύο δηλαδή τους
T(n-1)καιT(n-2). Για παράδειγμα γιαn = 5προκύπτει ότιT(n-1) = 4καιT(n-2)= 3. Συμπεραίνω ότι ο πρώτος όρος είναι ο μεγαλύτερος, οπότε προκύπτει ότιT(n) = T(n-1)+T(n-2)+1 ≤ T(n-1)+T(n-1)+1 - Λύνω την νέα αναδρομή που προέκυψε
A(n) = A(n-1)+A(n-1)+1 = 2A(n-1)+1
\(A(n)=2A(n-1)+1\)
\(A(n-1)=2[2A(n-2)+1]+1 = 2^2 Α(n-2) + 2 + 1\)
\(A(n-2) = 2[2^2A(n-2) + 2 + 1] + 1 = 2^3 Α(n-3) + 2^2 + 2 + 1\)
…
\(Α(n-k) = 2^k Α(n-3) + 2^{k-1} + … + 2^2 + 2 + 1\)
ΓιαA(0)σημαίνει ότιn-k = 0 ⇒ n = kάρα
\(Α(n) = 2^n Α(0) + 2^{n-1} + … + 2^2 + 2 + 1 = 2^n Α(0) + [2^{n-1} + … + 2^2 + 2 + 1]\)
Οι όροι μέσα στην αγκύλη, αποτελούν ένα άθροισμα γεωμετρικης προόδου και μπορούμε να το γράψουμε ως: \(2^0 + 2^1 + 2^2 + … + 2^{n-1}\)
Χρησιμοποιούμε τον τύπο: \( \Sigma m = \alpha \frac{r^m – 1}{r – 1} \)- O πρώτος όρος
(α)είναι το \(2^0 = 1\) - Ο λόγος
(r)είναι2(κάθε όρος είναι διπλάσιος του προηγούμενου). - Το πλήθος των όρων
(m)είναιn, διότι ξεκινάμε απο \(2^0\) και φτάνουμε μέχρι \(2^{n−1}\), άρα έχουμεn−1−0+1 = nόρους).
- O πρώτος όρος
- Αντικαθιστώντας στην αναδρομική εξίσωση, προκύπτει \(A(n) = 2^n \Theta(1) + \frac{2^{n-1+1} – 1}{2 – 1} = \Theta(2^n) \)
Ο αλγόριθμος έχει εκθετική πολυπλοκότητα γεγονός αρνητικό διότι θα απαιτεί πολύ χρόνο για την εκτέλεσή του
Εκτέλεση του αλγορίθμου και εμφάνιση απαιτούμενου χρόνου εκτέλεσης
Για την προσομείωση επιλέχθηκαν: (1) στο σύννεφο μέσω του Google Colab και (2) τοπικά με το Ms VsCode
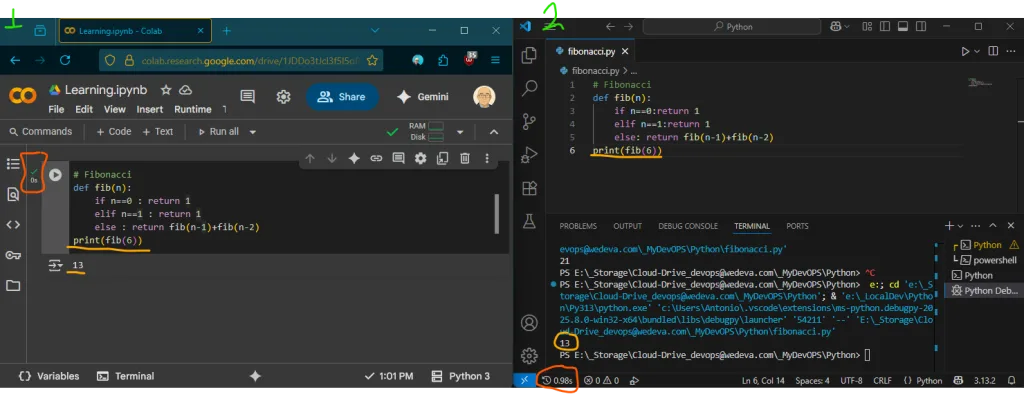
Για τον αριθμό έξι (6) παρατηρούμε:
- Colab (cloud): T(n) < 1 min απεικονιζεται ως 0s
- VsCode (local): T(n) < 1min απεικονιζεται ως 0.98s
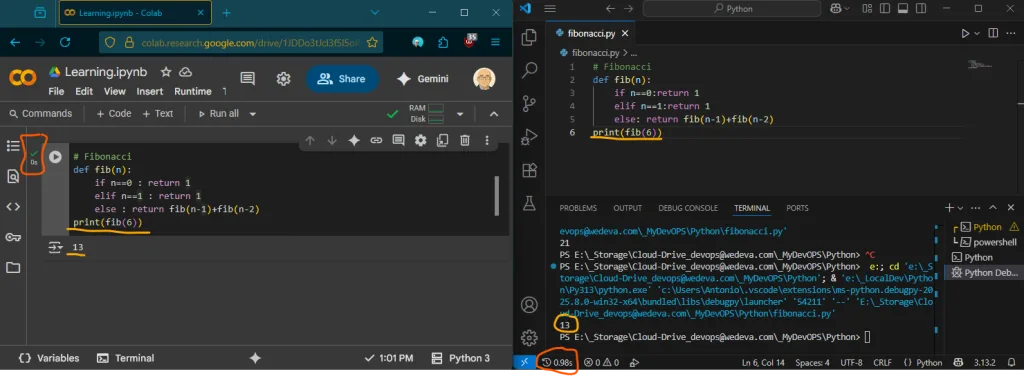
Για τον αριθμό τριάντα (30) παρατηρούμε:
- Colab (cloud): T(n) < 1 min απεικονιζεται ως 0s
- VsCode (local): T(n) = 1.19s
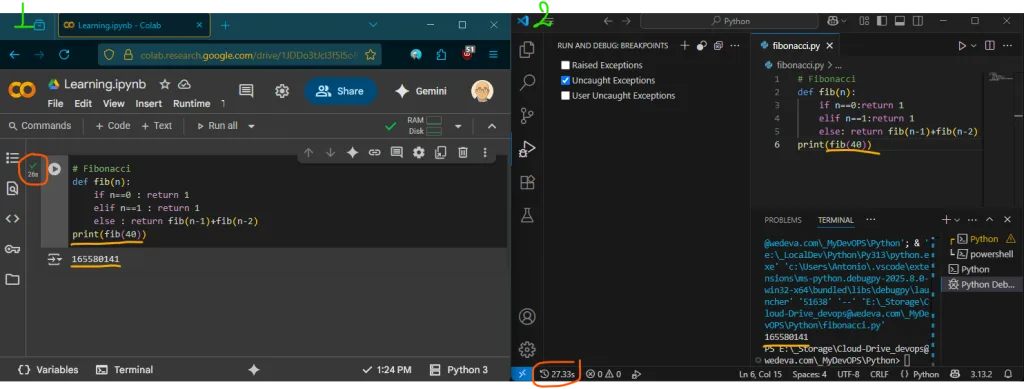
Για τον αριθμό σαράντα (40) παρατηρούμε:
- Colab (cloud): T(n) = 26s απεικονιζεται ως 0s
- VsCode (local): T(n) = 27.33s
Συμπέρασμα
Η εκτέλεση του παραπάνω αλγορίθμου Fibonacci (ως έχει) είναι καταστροφική για την απόδοση του συστήματος διότι για μεγάλους αριθμούς (μεγάλα n) η χρονική πολυπλοκότητα είναι εκθετική.
Σημείωση: ο χρόνος εκτέλεσης διαφέρει απο Colab (cloud) σε VsCode (local) γιατί είναι διαφορετική η διαθεσιμότητα πόρων (CPU, RAM) των δύο εργαλείων. Παρατηρήστε στην πορτοκαλί επισήμανση.
ΠΡΟΣΟΧΗ η χρονική πολυπλοκότητα ΔΕΝ αλλάζει!
Aνάλυση του Αναδρομικού Αλγορίθμου Fibonacci με Δέντρο Αναδρομης
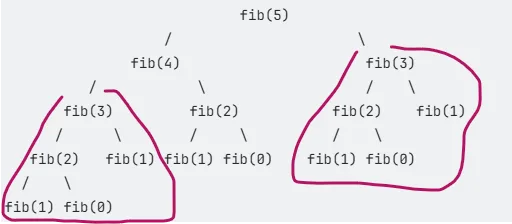
Παρατηρούμε τα εξής:
- Επανάληψη υπο-προβλημάτων: Για να υπολογίσουμε το
fib(5), πρέπει να υπολογίσουμε τοfib(4)και τοfib(3). Για να υπολογίσουμε τοfib(4), πάλι υπολογίζουμε τοfib(3)και τοfib(2). Βλέπουμε ότι τοfib(3)υπολογίζεται δύο φορές, τοfib(2)τρεις φορές, κ.ο.κ. Αυτή η επανάληψη είναι το κλειδί για την υψηλή πολυπλοκότητα. - Δέντρο κλήσεων: Ο τρόπος με τον οποίο γίνονται οι κλήσεις μοιάζει με ένα δυαδικό δέντρο, όπου κάθε κόμβος αντιπροσωπεύει μια κλήση της συνάρτησης
fib. Το βάθος του δέντρου είναι περίπουn.
Η μέθοδος του δέντρου αναδρομής είναι εξαιρετική για να οπτικοποιήσουμε την αναδρομική διαδικασία και να εντοπίσουμε τα σημεία όπου ο αλγόριθμος είναι αναποτελεσματικός (όπως οι επαναλαμβανόμενες κλήσεις στην περίπτωση του Fibonacci).
Η βελτιστοποίηση απόδοσης του αλγορίθμου μπορεί να γίνει με την χρήση του Δυναμικού Προγραμματισμού
Παραπομπές: ΠΛΗ30 – ΜΑΘΗΜΑ 2.2 – Δυναμικός Προγραμματισμός – Θεωρία 1 από 3 (Ακολουθία Fibonacci)